Реферат передача информации в социальных биологических и технических системах

метки: Информация, Передача, Технический, Социальный, Биологический, Система, Алгоритм, Количество

..

Подобный материал:

• , 191.28kb.
• , 592.28kb.
• , 262.31kb.
• , 237.91kb.
• , 2102.05kb.
• , 34.3kb.
• , 42.1kb.
• , 1995.16kb.
• , 49.99kb.
• , 32.08kb.

Примерные ответы на теоретические вопросы билетов по информатике.

Билет № 1

Понятие информации. Виды информационных процес­сов. Поиск и систематизация информации. Хранение ин­формации; выбор способа хранения информации. Пере­дача информации в социальных, биологических и технических системах.

«информация»

Все подходы к феномену информации имеют право на су­ществование и исследуются в соответствующих областях на­уки. «В информатике информацию можно рассматривать как продукт взаимодействия данных и методов их обработ­ки, адекватных решаемой задаче».

информацион­ный процесс

обработки информации

Поиск и отбор

Получение новой информации.

Получение новой по содержанию информации из исход­ной информации возможно путем как математических вычислений, так и логических рассуждений.

Структурирование, Кодирование

передачи информации

хранения информации

Коррекцию.

• Доступ. Организация оптимального доступа к различ­ной по ценности информации с использованием проце­дур защиты от несанкционированного доступа может быть отнесена к процессу хранения.

Билет №2

Понятие о кодировании информации. Выбор способа представления информации в соответствии с поставлен­ной задачей. Универсальность дискретного (цифрового) представления информации. Двоичное кодирование.

Информация никогда не появляется в «чистом виде», она всегда как-то представлена, в каком-либо формализованном (закодированном) виде. Одна и та же информация может быть представлена различными способами. От того, как представлена информация, зависит очень многое, от воз­можной интерпретации до возможности ее технической об­работки. Так что в практических задачах важно выбрать тот способ представления информации, который наиболее удо­бен и адекватен решаемой задаче.

ко­дирования,

Многие годы человечество работало с информацией, преж­де чем был изобретен компьютер. С появлением компьютера стало возможным автоматизировать процессы обработки, передачи и хранения информации. При кодировании инфор­мации для технических устройств удобно использовать ал­фавиты, состоящие всего из двух знаков. Такие алфавиты называют двоичными. Чем меньше знаков в алфавите, тем проще должна быть устроена «машина» для распознавания (дешифровки) информационного сообщения. Однако чем ме­ньше знаков в алфавите, тем большее их количество требу­ется для кодирования, следовательно, тем больше длина кода. Легко рассчитать количество М элементарных сообще­ний, которые можно закодировать, используя код постоян­ной длины п и алфавит из R знаков: М = R ⁿ . Длину кода рассчитывают по формуле п = [log _R M + 1]. Если мы исполь­зуем двоичный алфавит, то М = 2 ^п .

При конструировании компьютеров был выбран двоичный алфавит {0, 1}, что позволило использовать достаточно про­стые устройства для представления и автоматического распо­знавания программ и данных. Именно простота сделала этот принцип кодирования таким распространенным. Наряду с этим свойством двоичное кодирование обеспечивает удобство физической реализации, универсальность представления лю­бого вида информации, уменьшение избыточности сообще­ния, обеспечение защиты от случайных искажений или не­желательного доступа. Наиболее распространены кодировки компьютерных символов: ASCII, Winl251, КОИ-8.

Билет № 3

Вероятностный и алфавитный подходы к измерению ин­формации. Единицы измерения информации. Скорость передачи информации. Пропускная способность канала связи.

Различные подходы к измерению количества информа­ции в сообщении определяются различием подходов к опре­делению самого понятия «информация».

Чтобы измерить что-либо, необходимо ввести единицу из­мерения. Минимальная единица измерения информации — бит. Смысл данной единицы также различен в рамках раз­ных подходов к измерению информации. Выделяют три подхода.

1. Неизмеримость информации в быту

2. Вероятностный, или содержательный подход, Сообщение, уменьшающее неопределенность знания в 2 раза, несет один бит информации.

Например: при подбрасывании монеты может выпасть либо «орел», либо «решка». Это два возможных события. Они равновероятны. Сообщение о том, что произошло одно из двух равновероятных событий (например, выпала «реш­ка»), уменьшает неопределенность нашего знания (перед броском монеты) в два раза.

Математики рассматривают идеальный вариант, что воз­можные события равновероятны. Если даже события нерав­новероятны, то возможен подсчет вероятности выпадения каждого события.

Под неопределенностью знания здесь понимают количе­ство возможных событий, их может быть больше, чем два.

Например, количество оценок, которые может получить студент на экзамене, равно четырем. Сколько информации содержится в сообщении о том, что он получил «4»? Рассуж­дая, с опорой на приведенное выше определение, можем сказать, что если сообщение об одном из двух возможных событий несет 1 бит информации, то выбор одного из четы­рех возможных событий несет 2 бита информации. Можно прийти к такому выводу, пользуясь методом половинного деления. Сколько вопросов необходимо задать, чтобы выяс­нить необходимое, столько битов и содержит сообщение. Во­просы должны быть сформулированы так, чтобы на них можно было ответить «да» или «нет», тогда каждый из них будет уменьшать количество возможных событий в 2 раза.

Очевидна связь количества возможных равновероятных событий и количества информации:

Заполним по формуле таблицу:

Количество битов	0	1	2	3	4	5	6	7	8	9	10
Количество событий	1	2	4	8	16	32	64	128	256	512	1024

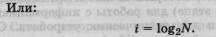
Это формула Р. Хартли. Если р = 1/N — вероятность на­ступления каждого из N равновероятных событий, тогда формула Хартли записыватся так:

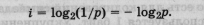
Чтобы пользоваться рассмотренным подходом, необходи­мо вникать в содержание сообщения. Это не позволяет ис­пользовать данный подход для кодирования и передачи ин­формации с помощью технических устройств.

3. Алфавитный подход к измерению информации.

Алфавит любого языка включает в себя конечный набор символов. Исходя из вероятностного подхода к определению количества информации, появление символов алфавита в тексте можно рассматривать как различные возможные со­бытия. Количество таких событий (символов) N называют мощностью алфавита. Тогда количество информации i, ко­торое несет каждый из JV символов, согласно вероятностно­му подходу определяется из формулы: N=2ⁱ

Количество символов в тексте из k символов: I=k*i

Алфавитный подход является объективным способом из­мерения информации и используется в технических устрой­ствах.

Переход к более крупным единицам измерения

Ограничения на максимальную мощность алфавита не су­ществует, но есть алфавит, который можно считать доста­точным (на современном этапе) для работы с информацией, как для человека, так и для технических устройств. Он включает в себя: латинский алфавит, алфавит языка стра­ны, числа, спецсимволы — всего около 200 знаков. По при­веденной выше таблице можно сделать вывод, что 7 битов информации недостаточно, требуется 8 битов, чтобы закоди­ровать любой символ такого алфавита, 256 = 2 ⁸ . 8 битов об­разуют 1 байт. То есть для кодирования символа компьютер­ного алфавита используется 1 байт. Укрупнение единиц из­мерения информации аналогично применяемому в физике — используют приставки «кило», «мега», «гига». При этом следует помнить, что основание не 10, а 2. 1 кило­байт (Кб) — это 2¹⁰ = 1024 байтов, 1 мегабайт (Мб) = = 2¹⁰ Кб = 2²⁰ байтов и т. д.

Умение оценивать количество информации в сообще­нии поможет определить скорость информационного пото­ка по каналам связи. Максимальную скорость передачи информации по каналу связи называют пропускной спо­собностью канала связи. Самым совершенным средством связи на сегодня являются оптические световоды. Инфор­мация передается в виде световых импульсов, посылае­мых лазерным излучателем. У этих средств связи высокая помехоустойчивость и пропускная способность более 100 Мбит/с.

Билет № 4

Понятие алгоритма: свойства алгоритмов, исполнители алгоритмов. Автоматическое исполнение алгоритма. Основные алгоритмические структуры.

Понятие алгоритма, Исторический обзор.

(algorismi)

Формализация понятия алгоритма., Определение 1.

Варианты словесного определения алгоритма, принадле­жащие российским ученым-математикам А. Н. Колмогоро­ву и А. А. Маркову:

Определение 2 (Колмогоров)., Определение 3 (Марков)., Свойства алгоритмов, Дискретность., Конечность., Точность (определенность)., Понятность., Универсальность (массовость).

исполнителя

Автоматическое исполнение алгоритма

Алгоритм позволяет формализовать выполнение процесса обработки исходных данных и получения результата. На этом основана работа программно управляемых исполните­лей-автоматов, например промышленных роботов. От испол­нителя не требуется понимания сущности алгоритма, он должен точно выполнять команды в заданной последова­тельности.

Примером исполнителя, автоматически выполняющего различные алгоритмы, является компьютер. Рассмотрим за­пись на жесткий диск компьютера телевизионной передачи с помощью ТВ-тюнера. Указав в расписании время начала и окончания записи, поставив «флажок» возле позиции «Вы­ключить компьютер после записи», пользователь может быть уверен, что передача будет записана и компьютер будет выключен. Всю заданную работу выполнит компьютер по разработанному ранее алгоритму, не внося никаких измене­ний (другая передача, другое время, невыключение компью­тера).

Способы описания алгоритмов

Словесное описание, Описание на алгоритмическом языке, Описание в графической форме в виде блок-схемы.

В схеме алгоритма каждому типу действий (ввод исходных данных, вычисление, проверка условия, управление цик­лом, вывод результатов, окончание) соответствует своя гео­метрическая фигура — блок. Блоки соединяются линиями со стрелками, указывающими последовательность действий. Форма блоков установлена ГОСТом. Внутри блока записыва­ется содержание соответствующего действия. Совокупность блоков образует блок-схему алгоритма. (В Microsoft Office можно использовать готовые шаблоны блоков.)

Основные блоки,

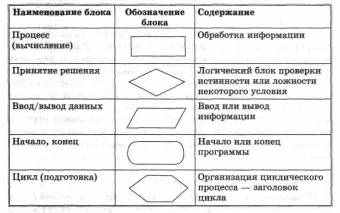
Описание в виде программы для компьютера на языке программирования, Основные алгоритмические структуры

Алгоритм может быть реализован в виде комбинации трех базовых алгоритмических конструкций: линейной, разветвленной, циклической.

Алгоритм линейной структуры, Алгоритм разветвленной структуры

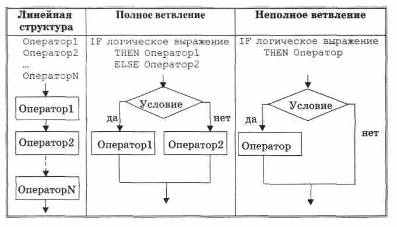
Алгоритм циклической структуры

Если количество повторений известно, то используют цикл со счетчиком, иначе — цикл с предварительной или последующей проверкой условия повторения.

Циклическую структуру реализуют операторы трех типов.

Оператор FOR…DO действует следующим образом. Тело цикла выполняется для каждого значения параметра цикла / от его начального Ml до конечного значения М2 включи­тельно. J, Ml, M2 — чаще всего переменные целого типа. Шаг изменения переменной цикла / равен +1 или -1.

Оператор WHILE…DO действует следующим образом. Каж­дый раз предварительно проверяется значение логического выражения. Пока оно истинно, выполняется тело цикла. Как только оно становится ложным, происходит выход за пределы цикла. Если с самого начала значение логического выражения является ложным, то тело цикла не выполняется ни разу.

Оператор REPEAT…UNTIL действует следующим образом. Тело цикла выполняется, пока значение логического выраже­ния ложно. Тело цикла выполняется как минимум один раз.

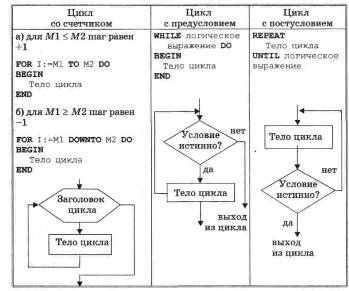
Все алгоритмические конструкции имеют общее свойст­во: один вход и один выход. Допускается неограниченное со­единение структур и их вложение друг в друга, что позволя­ет проектировать сложные алгоритмы.