Кластерный анализ

метки: Кластерный, Анализ, Психология, Использование, Кластеризация, Объект, Кластер, Группа

(англ. Data clustering ) — задача разбиения заданной выборки объектов (ситуаций) на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Задача кластеризации относится к статистической обработке, а также к широкому классу задач обучения без учителя. Кластерный анализ — это многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы (кластеры)(Q-кластеризация, или Q-техника, собственно кластерный анализ).

Кластер — группа элементов, характеризуемых общим свойством, главная цель кластерного анализа — нахождение групп схожих объектов в выборке (примечание 1).

Спектр применений кластерного анализа очень широк: его используют в археологии, медицине, психологии, химии, биологии, государственном управлении, филологии, антропологии, маркетинге, социологии и других дисциплинах. «Тематика исследований варьирует от анализа морфологии мумифицированных грызунов в Новой Гвинее до изучения результатов голосования сенаторов США, от анализа поведенческих функций замороженных тараканов при их размораживании до исследования географического распределения некоторых видов лишая в Саскачеване» (примечание 1).

Однако универсальность применения привела к появлению большого количества несовместимых терминов, методов и подходов, затрудняющих однозначное использование и непротиворечивую интерпретацию кластерного анализа.

1. Задачи и условия

основные задачи

• Разработка типологии или классификации.
• Исследование полезных концептуальных схем группирования объектов.
• Порождение гипотез на основе исследования данных.
• Проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных (примечание 1).

следующие этапы

• Отбор выборки для кластеризации.
• Определение множества переменных, по которым будут оцениваться объекты в выборке.
• Вычисление значений той или иной меры сходства между объектами.
• Применение метода кластерного анализа для создания групп сходных объектов.
• Проверка достоверности результатов кластерного решения (примечание 1).
  13 стр., 6394 слов

  Математические методы исследования в обработке эмпирических данных ...

  ... многомерное шкалирование; многомерный анализ данных (факторный, кластерный); дисперсионный анализ; анализ данных на компьютере, статистические пакеты; приближенные вычисления; возможности и ограничения конкретных компьютерных методов обработки данных; стандарты обработки данных; нормативы представления результатов анализа данных в научной психологии; методы математического моделирования; модели ...

требования к данным

1. показатели не должны коррелировать между собой
2. показатели должны быть безразмерными
3. распределение показателей должно быть близко к нормальному
4. показатели должны отвечать требованию «устойчивости», под которой понимается отсутствие влияния на их значения случайных факторов
5. выборка должна быть однородна, не содержать «выбросов» (примечание 2).

Если кластерному анализу предшествует факторный анализ, то выборка не нуждается в «ремонте» — изложенные требования выполняются автоматически самой процедурой факторного моделирования (есть ещё одно достоинство — z-стандартизация без негативных последствий для выборки; если её проводить непосредственно для кластерного анализа, она может повлечь за собой уменьшение чёткости разделения групп).

В противном случае выборку нужно корректировать.

2. Анализ и интерпретация его результатов

При анализе результатов социологических исследований рекомендуется осуществлять анализ методами иерархического агломеративного семейства, а именно методом Уорда, при котором внутри кластеров оптимизируется минимальная дисперсия, в итоге создаются кластеры приблизительно равных размеров. Метод Уорда наиболее удачен для анализа социологических данных. В качестве меры различия лучше квадратичное евклидово расстояние, которое способствует увеличению контрастности кластеров (примечание 1).

Главным итогом иерархического кластерного анализа является дендрограмма или «сосульчатая диаграмма». При её интерпретации исследователи сталкиваются с проблемой того же рода, что и толкование результатов факторного анализа — отсутствием однозначных критериев выделения кластеров. В качестве главных рекомендуется использовать два способа — визуальный анализ дендрограммы и сравнение результатов кластеризации, выполненной различными методами (примечание 1; примечание 2).

Визуальный анализ дендрограммы предполагает «обрезание» дерева на оптимальном уровне сходства элементов выборки. «Виноградную ветвь» (терминология Олдендерфера М. С. и Блэшфилда Р. К.) целесообразно «обрезать» на отметке 5 шкалы Rescaled Distance Cluster Combine, таким образом будет достигнут 80 % уровень сходства. Если выделение кластеров по этой метке затруднено (на ней происходит слияние нескольких мелких кластеров в один крупный), то можно выбрать другую метку. Такая методика предлагается Олдендерфером и Блэшфилдом (примечание 1).

Теперь возникает вопрос устойчивости принятого кластерного решения. По сути, проверка устойчивости кластеризации сводится к проверке её достоверности. Здесь существует эмпирическое правило — устойчивая типология сохраняется при изменении методов кластеризации. Результаты иерархического кластерного анализа можно проверять итеративным кластерным анализом по методу k-средних. Если сравниваемые классификации групп респондентов имеют долю совпадений более 70 % (более 2/3 совпадений), то кластерное решение принимается.

Анализ взаимосвязи философии и науки

... реферате сопоставлены философия и наука, рассмотрены основные исторические типы отношения философии и науки. Работа демонстрирует сложность их взаимосвязи. Показана специфика философской методологии науки с рассмотрением концепций науки ... над фактами и привносились в науку извне. Односторонне используя метод дедукции, объясняя конкретные свойства объектов при помощи общих принципов, сторонники ...

Проверить адекватность решения, не прибегая к помощи другого вида анализа, нельзя. По крайней мере, в теоретическом плане эта проблема не решена. В классической работе Олдендерфера и Блэшфилда «Кластерный анализ» подробно рассматриваются и в итоге отвергаются дополнительные пять методов проверки устойчивости: 1) кофенетическая корреляция — не рекомендуется и ограниченна в использовании; 2) тесты значимости (дисперсионный анализ) — всегда дают значимый результат; 3) методика повторных (случайных) выборок, что, тем не менее, не доказывает обоснованность решения; 4) тесты значимости для внешних признаков пригодны только для повторных измерений; 5) методы Монте-Карло очень сложны и доступны только опытным математикам (примечание 1).

3. Типология задач кластеризации

3.1. Типы входных данных

• Признаковое описание объектов. Каждый объект описывается набором своих характеристик, называемых признаками . Признаки могут быть числовыми или нечисловыми.
• Матрица расстояний между объектами. Каждый объект описывается расстояниями до всех остальных объектов обучающей выборки.

3.2. Цели кластеризации

• Понимание данных путём выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа (стратегия «разделяй и властвуй»).

• Сжатие данных. Если исходная выборка избыточно большая, то можно сократить её, оставив по одному наиболее типичному представителю от каждого кластера.
• Обнаружение новизны (англ. novelty detection ).

  Выделяются нетипичные объекты, которые не удаётся присоединить ни к одному из кластеров.

В первом случае число кластеров стараются сделать поменьше. Во втором случае важнее обеспечить высокую степень сходства объектов внутри каждого кластера, а кластеров может быть сколько угодно. В третьем случае наибольший интерес представляют отдельные объекты, не вписывающиеся ни в один из кластеров.

Во всех этих случаях может применяться иерархическая кластеризация, когда крупные кластеры дробятся на более мелкие, те в свою очередь дробятся ещё мельче, и т. д. Такие задачи называются задачами таксономии.

Результатом таксономии является древообразная иерархическая структура. При этом каждый объект характеризуется перечислением всех кластеров, которым он принадлежит, обычно от крупного к мелкому.

Классическим примером таксономии на основе сходства является биноминальная номенклатура живых существ, предложенная Карлом Линнеем в середине XVIII века. Аналогичные систематизации строятся во многих областях знания, чтобы упорядочить информацию о большом количестве объектов.

3.3. Методы кластеризации

• K-средних (K-means)
• Графовые алгоритмы кластеризации
• Статистические алгоритмы кластеризации
• Алгоритмы семейства FOREL
• Иерархическая кластеризация или таксономия
• Нейронная сеть Кохонена
• Ансамбль кластеризаторов
• Алгоритмы семейства КRAB
• EM-алгоритм
• Алгоритм, основанный на методе просеивания

Количественные и качественные методы анализа данных в социологии

... объектов социологического исследования, повышая информативность выводов и даже серьезно изменяя их. Можно выделить две основные проблемы социологического исследования, основанного только на анализе статистических данных: ... как количественные указывают на масштаб, объем, интенсивность характеристик изучаемого явления. Качественные данные позволяют раскрыть значения социального явления, количественные ...

4. Формальная постановка задачи кластеризации

кластерами

Алгоритм кластеризации

Кластеризация (обучение без учителя) отличается от классификации (обучения с учителем) тем, что метки исходных объектов изначально не заданы, и даже может быть неизвестно само множество .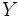

Решение задачи кластеризации принципиально неоднозначно, и тому есть несколько причин:

• не существует однозначно наилучшего критерия качества кластеризации. Известен целый ряд эвристических критериев, а также ряд алгоритмов, не имеющих чётко выраженного критерия, но осуществляющих достаточно разумную кластеризацию «по построению». Все они могут давать разные результаты.
• число кластеров, как правило, неизвестно заранее и устанавливается в соответствии с некоторым субъективным критерием.
• результат кластеризации существенно зависит от метрики, выбор которой, как правило, также субъективен и определяется экспертом.

5. Применение

5.1. В биологии

В биологии кластеризация имеет множество приложений в самых разных областях. Например, в биоинформатике с помощью нее анализируются сложные сети взаимодействующих генов, состоящие порой из сотен или даже тысяч элементов. Кластерный анализ позволяет выделить подсети, узкие места, концентраторы и другие скрытые свойства изучаемой системы, что позволяет в конечном счете узнать вклад каждого гена в формирование изучаемого феномена.

5.2. В социологии

5.3. В информатике

• Группирование результатов поиска : Кластеризация используется для «интеллектуального» группирования результатов при поиске файлов, веб-сайтов, других объектов, предоставляя пользователю возможность быстрой навигации, выбора заведомо более релевантного подмножества и исключения заведомо менее релевантного — что может повысить юзабилити интерфейса по сравнению с выводом в виде простого сортированного по релевантности списка.
  • Clusty[1] — кластеризующая поисковая машина компании Vivísimo
  • Nigma — российская поисковая система с автоматической кластеризацией результатов
  • Quintura — визуальная кластеризация в виде облака ключевых слов

• Сегментация изображений (image segmentation) : Кластеризация может быть использована для разбиения цифрового изображения на отдельные области с целью обнаружения границ (edge detection) или распознавания объектов.

• Интеллектуальный анализ данных (data mining) : Кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель для всех данных. Таким приемом постоянно пользуются в маркетинге, выделяя группы клиентов, покупателей, товаров и разрабатывая для каждой из них отдельную стратегию.

Многомерный анализ данных

... характеризующихся несколькими качественными или количественными признаками, используют методы многомерного анализа данных, в частности факторного и кластерного анализа. Факторный анализ применяют в составлении опросников и анализе данных, полученных в результате исследования. Он необходим для сокращения числа ...

Литература

[Электронный ресурс]//URL: https://psystars.ru/referat/klasternyiy-analiz-v-psihologii/

• Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: классификация и снижение размерности. — М.: Финансы и статистика, 1989.
• Журавлев Ю. И., Рязанов В. В., Сенько О. В. «Распознавание». Математические методы. Программная система. Практические применения. — М.: Фазис, 2006. ISBN 5-7036-0108-8.
• Загоруйко Н. Г. Прикладные методы анализа данных и знаний. — Новосибирск: ИМ СО РАН, 1999. ISBN 5-86134-060-9.
• Мандель И. Д. Кластерный анализ. — М.: Финансы и статистика, 1988. ISBN 5-279-00050-7.
• Паклин Н.Б., Орешков В.И. Бизнес-аналитика: от данных к знаниям (+ СD).

  -СПб: Питер, 2009. ISBN 978-5-49807-257-9

• Хайдуков Д. С. Применение кластерного анализа в государственном управлении// Философия математики: актуальные проблемы. – М.: МАКС Пресс, 2009.
• Шлезингер М., Главач В. Десять лекций по статистическому и структурному распознаванию. — Киев: Наукова думка, 2004. ISBN 966-00-0341-2.
• Hastie, T., Tibshirani R., Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. — 2nd ed. — Springer-Verlag, 2009. — 746 p. — ISBN 978-0-387-84857-0 .
• Jain, Murty, Flynn Data clustering: a review. // ACM Comput. Surv. 31 (3) , 1999
• Олдендерфер М. С., Блэшфилд Р. К. «Кластерный анализ» / «Факторный, дискриминантный и кластерный анализ»: пер. с англ.; Под. ред. И. С. Енюкова. — М.: «Финансы и статистика», 1989—215 с.
• Шуметов В. Г. Шуметова Л. В. «Кластерный анализ: подход с применением ЭВМ». ОрелГТУ, Орел, 2000. — 118 с.
• Электронный учебник по статистике. Москва, StatSoft. WEB: www.statsoft.ru/home/textbook/default.htm.

Данный реферат составлен на основе .